Teoría de conjuntos. Conceptos básicos YouTube
TEORÍA DE CONJUNTOS Explicación sencilla para Primaria YouTube

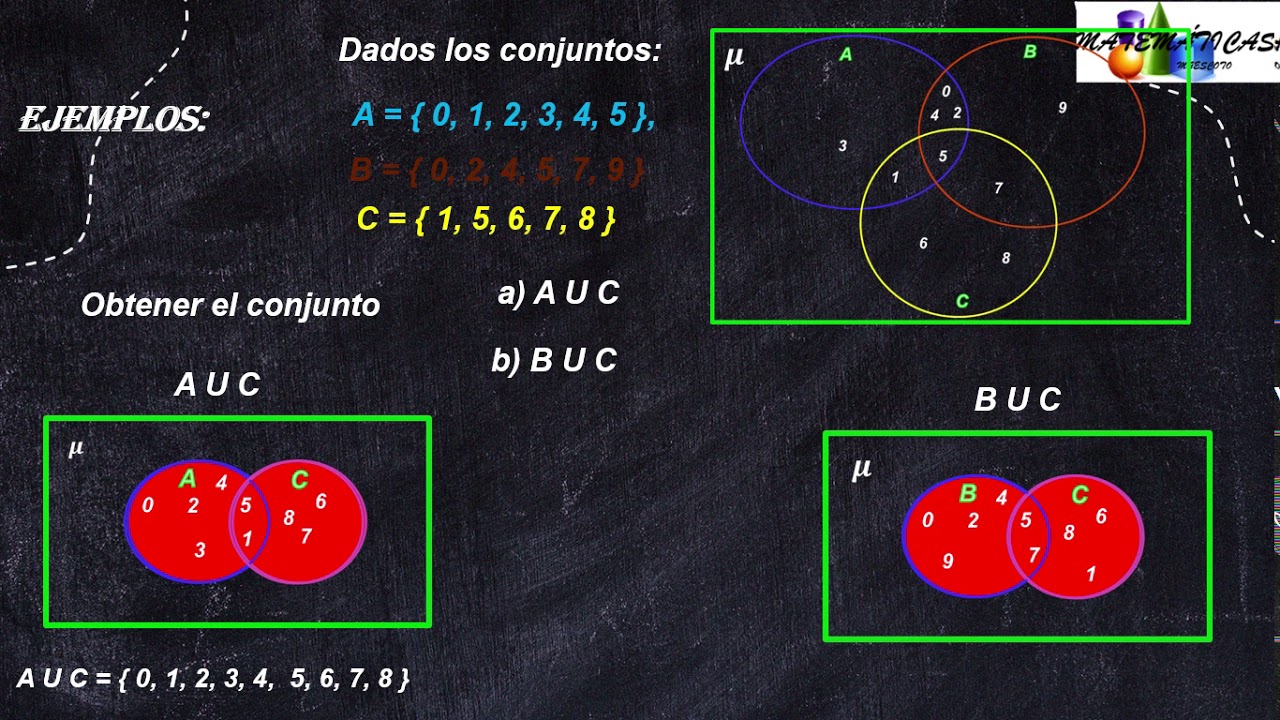
En la teoría de conjuntos, existen varias operaciones que se pueden realizar con conjuntos, como la unión, la intersección y la diferencia. Unión: La unión de dos conjuntos A y B, denotada por A ∪ B, es el conjunto que contiene todos los elementos que pertenecen a A o a B o a ambos conjuntos. Por ejemplo, si A = {1, 2, 3} y B = {3, 4, 5.
De Conjunto Teor 237 A De Conjuntos Conceptos B 225 Sicos Youtube, Complemento De Un Conjunto

Teoría de conjuntos. Un diagrama de Venn que ilustra la intersección de dos conjuntos. La teoría de conjuntos es una rama de la lógica matemática que estudia las propiedades y relaciones de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una.
TEORÍA DE CONJUNTOS, PROBABILIDAD Y ESTADÍSTICA YouTube
La teoría de conjuntos es una rama de las matemáticas (y de la lógica) que se dedica a estudiar las características de los conjuntos y las operaciones que pueden efectuarse entre ellos. Es decir, la teoría de conjuntos es un área de estudio enfocada en los conjuntos. Por tanto, se encarga de analizar tanto los atributos que poseen, como.
Teoría de Conjuntos Teoría de Conjuntos
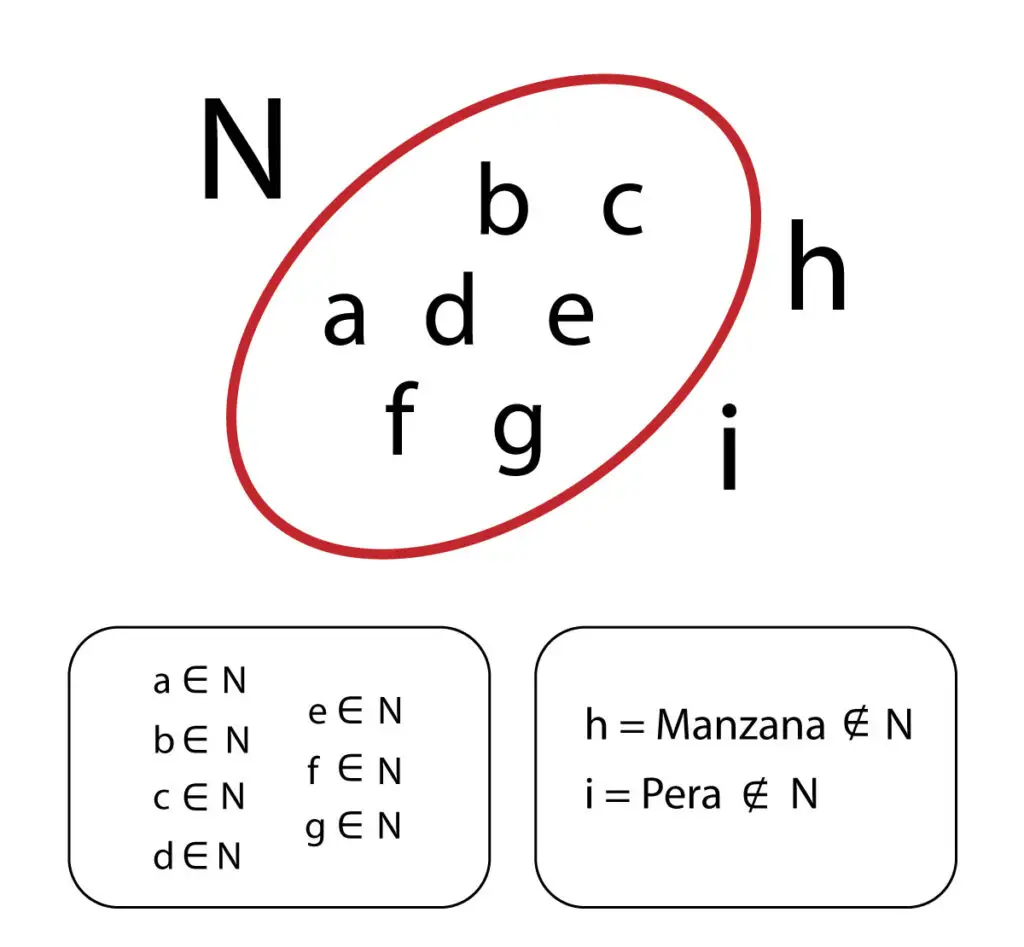
Pertenecía en la teoría de conjuntos. Cuando decimos que un elemento está dentro de un conjunto, nos referimos que dicho elemento pertenece al conjunto, para indicar que pertenece se utiliza el símbolo ∈.Ahora, cuando un elemento no está dentro del conjunto, nos referimos a que el elemento no pertenece al conjunto y para indicarlo utilizamos ∉.
Teoría de conjuntos Definición y como se representa

La teoría de conjuntos es una rama de las matemáticas que se encarga del estudio de las propiedades y relaciones entre conjuntos. Los conjuntos son una colección de objetos o elementos que comparten una característica en común.
Teoria de conjuntos YouTube

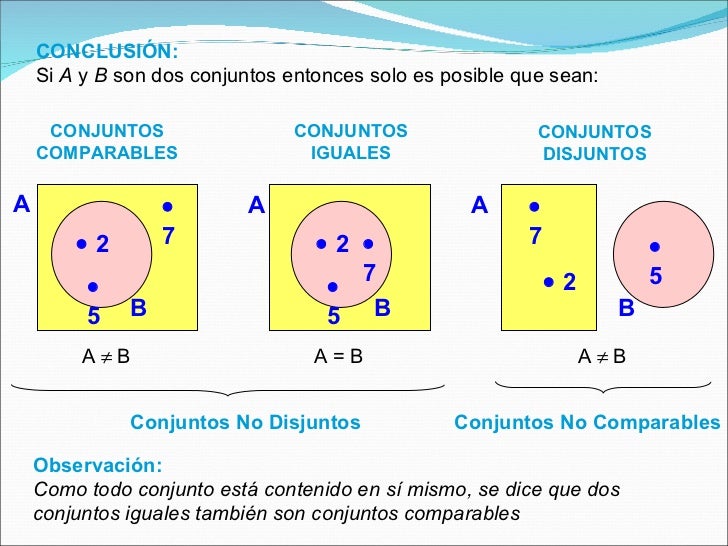
Dos conjuntos y son iguales si y solo si y. Si y no es igual, decimos que es un subconjunto propio de, y escribimos. El conjunto se llama el conjunto vacío. Este conjunto claramente no tiene elementos. Usando Teorema 1.1.1, es fácil demostrar que todos los conjuntos sin elementos son iguales. Así, nos referimos al conjunto vacío.
PPT Teoría de Conjuntos PowerPoint Presentation, free download ID4950525
En la teoría de conjuntos, son "set", "element" y "membership". Estos conceptos (más o menos) se corresponden entre sí. En la mayoría de los libros, un conjunto se denota ya sea usando la letra M (que significa la palabra alemana "menge") o letras romanas mayúsculas del alfabeto temprano — ABC ,,, etcétera.
INTERSECCIÓN DE CONJUNTOS MATEMÁTICA DIAGRAMA DE VENN YouTube

La teoría de los conjuntos es lo suficientemente flexible y general como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, etc; gracias a las herramientas de la lógica, permite estudiar los fundamentos. Además, la propia teoría de conjuntos es objeto de estudio per se.
CONJUNTOS, TEORÍA, EJERCICIOS Y PROBLEMAS MATEMÁTICA OPERACIONES COMBINADAS CON DOS CONJUNTOS

La teoría de conjuntos, es tan simple como interesante y es una de las ramas fundamentales de las matemáticas, pues será fundamento -entre otros- de temas tan importantes como el concepto de funciones lineales. En una primera instancia, hemos de dejar claro el concepto de conjunto en matemáticas, para luego pasar a aprender cómo se definen.
1 TeoríA De Conjuntos
La teoría de conjuntos describe algunas ideas muy fundamentales e intuitivas sobre cómo las cosas llamadas «elementos» o «miembros» encajan en grupos. A pesar de la aparente simplicidad de las ideas, la teoría de conjuntos es bastante rigurosa. Al tratar de eliminar toda arbitrariedad en sus teorías, los matemáticos han afinado la.
OPERACIONES CON CONJUNTOS UNIÓN INTERSECCIÓN Y DIFERENCIA EXPLICACIONES BÁSICAS PDF
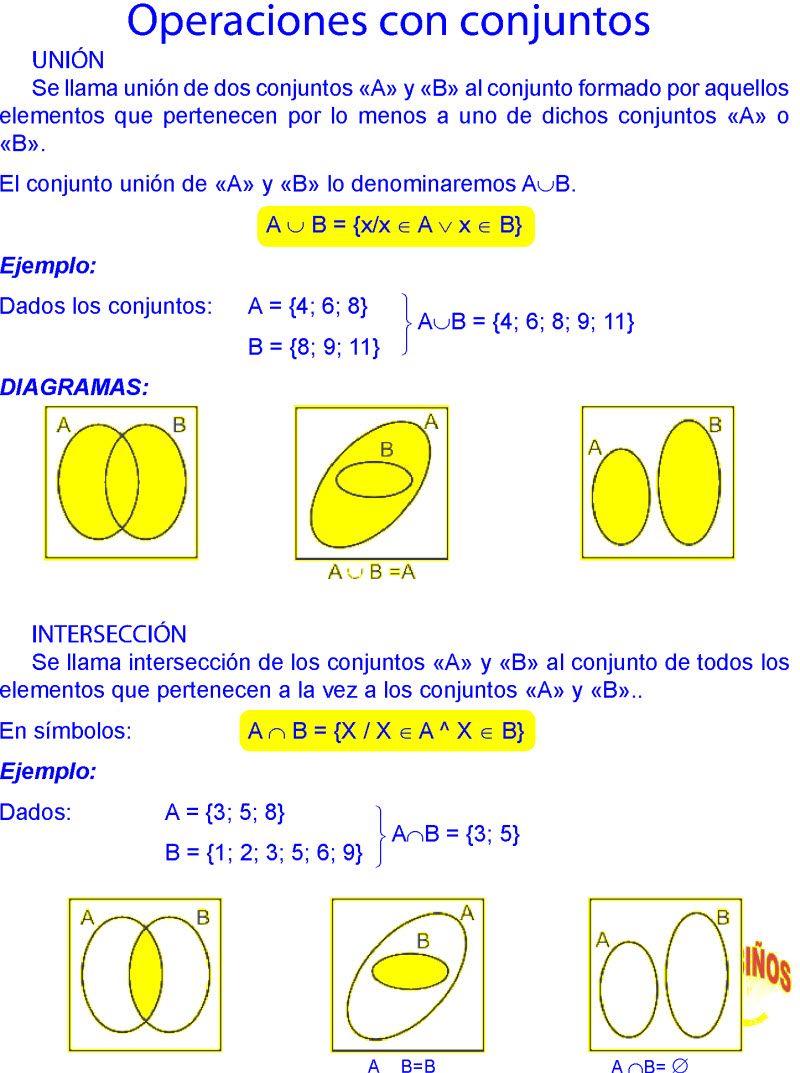
Un conjunto es una colección de objetos bien definidos y diferenciados entre sí. Estos objetos pueden ser concretos (números, letras) o abstractos (ideas, conceptos). Los conjuntos se denotan con letras mayúsculas A, B, C, etc. Los elementos se escriben dentro de llaves {}, separados por comas. Ejemplos: A = {1, 2, 3} B = {a, b, c}
Teoria De Conjuntos

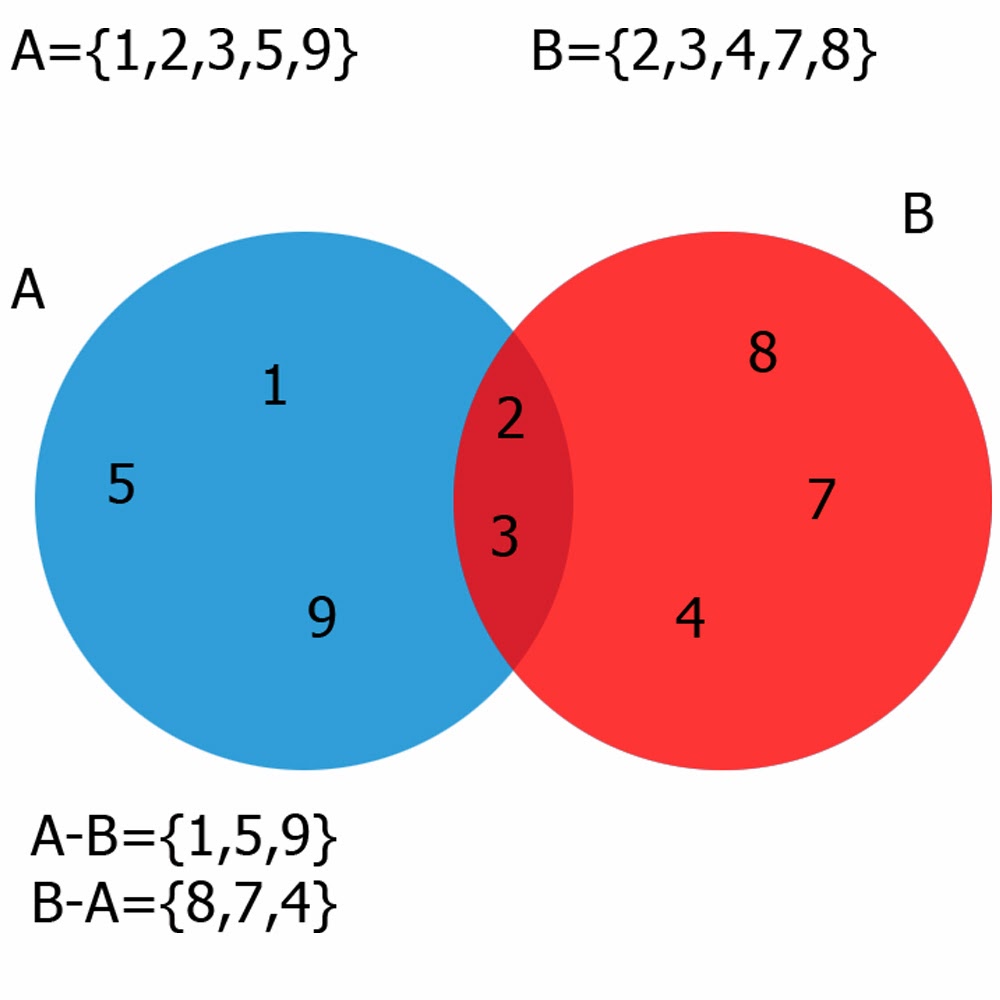
La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades y relaciones entre conjuntos, que son colecciones de objetos. Los símbolos más comunes son ∈ (pertenencia), ⊆ (subconjunto), ∪ (unión) y ∩ (intersección). Por ejemplo, si tenemos los conjuntos A = {1, 2, 3} y B = {2, 3, 4}, la intersección A ∩ B.
🔴🟢 TEORIA DE CONJUNTOS 2 CONJUNTOS en INTERSECCIÓN Juliana la Profe YouTube

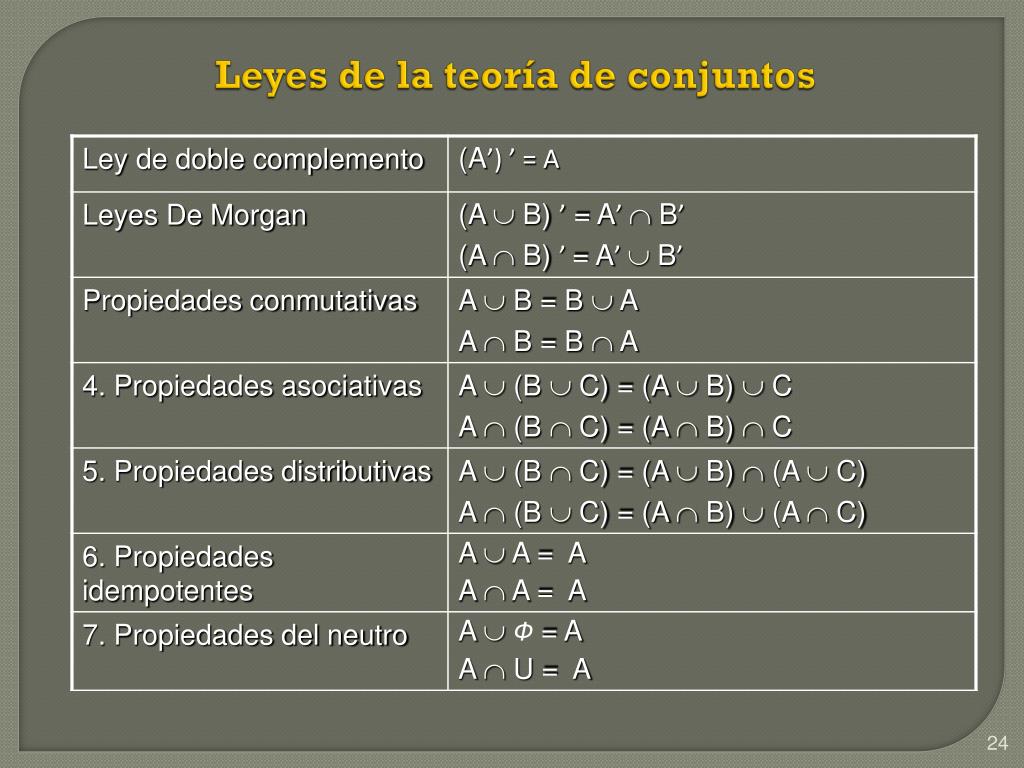
Ejercicio 4.2.3 4.2. 3. Demostrar lo siguiente utilizando las leyes de teoría de conjuntos, así como cualquier otro teorema probado hasta el momento. A ∪ (B − A) = A ∪ B A ∪ ( B − A) = A ∪ B. A − B = Bc −Ac A − B = B c − A c. A ⊆ B, A ∩ C ≠ ∅ ⇒ B ∩ C ≠ ∅ A ⊆ B, A ∩ C ≠ ∅ ⇒ B ∩ C ≠ ∅.
Teoría de conjuntos Definición y como se representa
Compartir Imprimir Citar. La teoría de conjuntos es la rama de la lógica matemática que estudia conjuntos, que pueden describirse informalmente como colecciones de objetos. Aunque los objetos de cualquier tipo se pueden reunir en un conjunto, la teoría de conjuntos, como rama de las matemáticas, se ocupa principalmente de aquellos que son.
2) Teoría de Conjuntos Conjunto (Matemáticas) Objetos matemáticos

Y en general se reconoce que fue Georg Cantor (1845-1918) el fundador de la teoría de conjuntos, en particular de los temas de conjuntos infinitos y sus propiedades, los cuales se abordan en este pequeño manual. Nuestro objetivo es ofrecer un panorama general de la teoría de conjuntos. Para ello se presentarán los más relevantes tipos de.
Teoría de Conjuntos I Conjunto (Matemáticas) Física y matemáticas

la teoría de conjuntos es una rama fundamental de las matemáticas que permite la formalización de muchos conceptos fundamentales en las ciencias y la vida diaria. A través de ella, podemos comprender mejor las relaciones entre los objetos y su clasificación, lo que nos permite hacer predicciones precisas y tomar decisiones informadas.